专家混合模型 (MoE)快速指南
专家混合 (MoE) 已成为一种流行的提高 LLM 效率的架构组件。在这篇博文中，我们将探讨研究人员在实现专家完美混合的道路上所采取的步骤。
MoE 已用于 Mixtral、DeepSeek-V2、Qwen2–57B-A14B 和 Jamba 等模型。但是，与任何架构组件一样，它具有超参数（专家总数、活跃专家数量、粒度），这些超参数会影响最终模型质量。
1、MoE 简介
在 GPU 和数据密集型 LLM 的世界中，在各种宝贵资源之间找到平衡非常重要。例如，如果我们希望 LLM 在各种任务中表现出色，可以通过增加参数数量来实现，这反过来会使推理（以及训练）更耗费计算资源。
MoE 的出现是为了创建一个规模大、能力强但在推理阶段要求稍低的 LLM。 MoE 建议拥有多个（例如 8 个）独立版本的前馈块 (FFN) — “专家” — 以及一个路由器，该路由器决定针对每个特定 token 使用哪个（例如 2 个）专家。
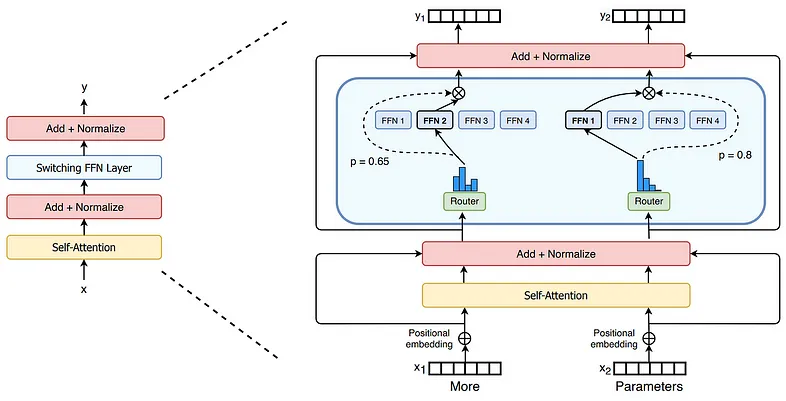
你可能会问，“为什么只使用 FFN，而不使用自注意力？”自注意力太复杂了，FFN 块通常包含所有 LLM 参数的一半以上。
第一个具有 MoE 的 LLM 是 Mixtral-8×7B（读作“具有 7B 基础模型的 8 个专家”），它是通过生成 Mistral 的每个 FFN 块的 8 个副本并添加为每个 token 选择 2 个专家的路由机制从 Mistral-7B 创建的。与 Mistral 的 7B 参数相比，它：
- 拥有 47B 参数，在创建时能够与 70B 模型相媲美，但
- 仅使用 13B 活动参数，使其比类似大小的同类模型更高效。
Mixtral 计算的专家权重如下：
最终输出等于：
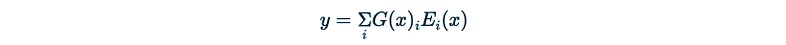
请注意 𝐻(𝑥)ᵢ 中的随机加数，它可作为训练稳定性的正则化器。
这仅在路由器平衡时才有效，这意味着它不会偏袒或忽视某些专家。否则，效率可能会受到阻碍而不是提高。特殊的“技巧”，包括辅助平衡损失函数，用于保持一切正常运行。此外，考虑到当前 token 的路由器分配，Mixtral 的 MoE 机制会尝试将传入的批次划分为几乎相等的部分，而开销不会大于预设的容量因子（通常约为 1-1.25）：
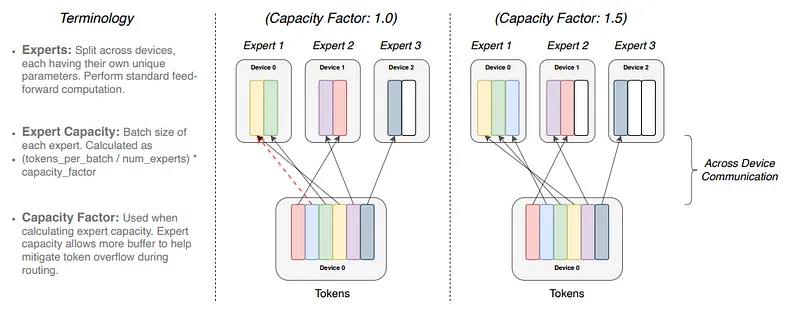
每个专家处理由容量因子调制的固定批量大小的 token。每个 token 都会路由到具有最高路由器概率的专家，但每个专家的批量大小固定为（总 token 数/专家数）×容量因子。如果 token 分配不均，则某些专家会溢出（用红色虚线表示），导致这些 token 不会被该层处理。更大的容量因子可以缓解此溢出问题，但也会增加计算和通信成本（用填充的白色/空槽表示）。
查看上面提到的 Hugging Face 帖子了解更多详情。
注意：MoE LLM 也称为稀疏模型，而非 MoE 模型则称为密集模型。
2、我们需要更多专家
Mixtral 只有 8 位专家，但后来的模型走得更远。
例如，DeepSeek-V2 有 2 位共享专家和 160 位路由专家，其中每个 token 选择 6 位。在总共 236B 个参数的情况下，每个 token 只激活了 21B 个。共享专家总是被调用；据说它们可以捕获不同上下文中的共同知识。路由专家很多，其中一些专家非常专业。
最近的几篇论文研究了具有越来越多专家的 MoE LLM 的行为，有充分的理由相信拥有许多专家是有益的。我将提到两篇研究相关经验规模定律的论文：
路由语言模型的规模定律（Scaling Law）本文表明，随着专家数量的增加，验证损失趋于改善：
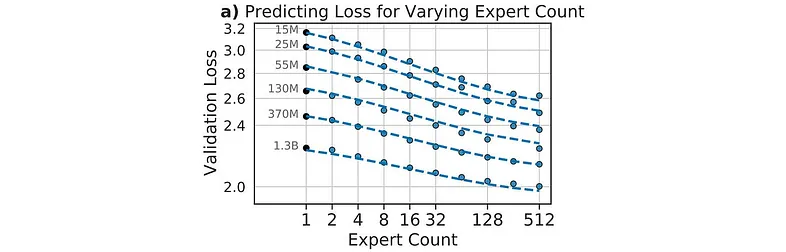
作者还研究了有效参数数量。例如，如果假设的 Mistral-cB 能够提供与 Mixtral 相同的质量，则 cB（c 十亿）是 Mixtral-8×7B 的有效参数数量。研究人员发现，随着基础模型规模的增加，有效参数数量的增益会减少：如果 Mistral 有 1T 个参数而不是 7B 个参数，那么用它创建 Mixtral-8×1T 不会提高质量（同一篇论文）：
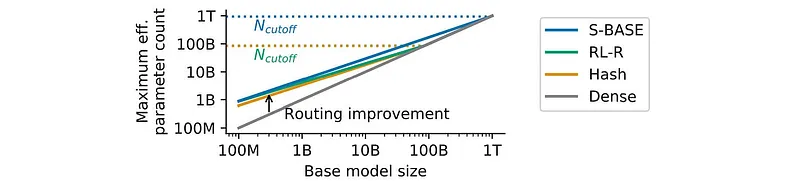
此处，S-BASE、RL-R 和 Hash 代表在专家之间更均匀地分配批次的不同方式。
结论：拥有更多专家是有益的，尽管增益会随着基础模型规模的增加而减少。
这种方法可能会因对所有模型规模使用相同的训练数据集而受到批评；这将在下一篇论文中讨论。
下一篇论文细粒度混合专家的规模定律采取了两个重要步骤。
首先，它寻求所有模型的最佳训练数据集大小。其次，它引入了专家粒度的概念。再次想象一下 Mistral-7B，我们正在将其转变为 MoE 模型。最初，它变成有 8 个专家的 Mixtral-8×7B，每个专家输出 d 维向量。现在，让我们将每个专家分成 G 个较小的专家，输出维度为 d/G 的向量：
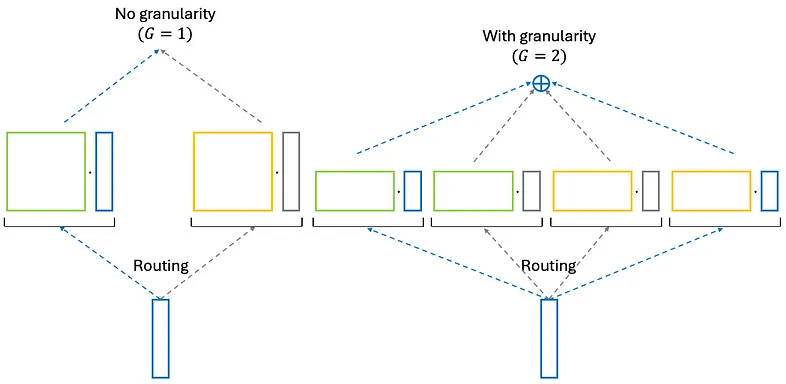
如果 G = 2，则每个原始专家将变成两个细粒度专家。此外，路由器现在将不是从 8 个专家中选择 2 个，而是从 16 个专家中选择 4 个。
现在，本文研究规模定律作为以下参数的平衡：
- 总训练计算量（以 FLOP 为单位）（取决于模型大小和数据集大小）、
- 基础模型大小、
- 专家数量、
- 专家粒度、
- 验证损失。
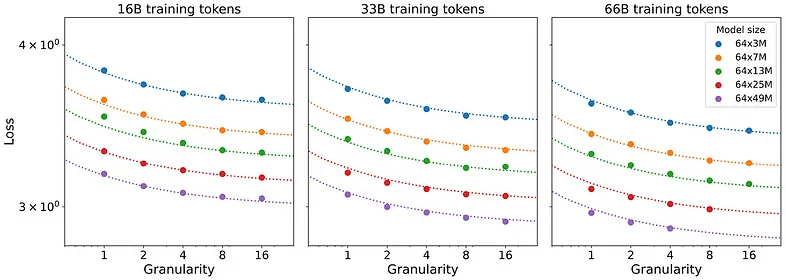
粒度是一个重要的超参数。随着基础模型大小的增加，增加粒度似乎有益（此处，N 是模型大小，D 是训练数据集大小（以 token 为单位）：
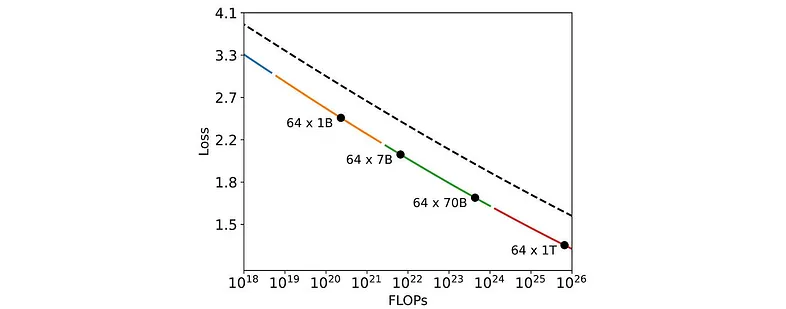
增加专家数量也有好处：
问题是，增加专家数量和粒度最终可能会阻碍模型效率，如下图所示：
此处，对于 G = 16，路由成本主导粒度收益。过于复杂的路由也会使推理速度变慢。
要点：如果我们及时增加粒度，MoE 会稳步提高质量，直到路由复杂性干扰。
3、如果我们有一百万个小专家怎么办？
从上一篇论文的角度来看，只要优化路由过程，随着我们增加专家数量和粒度，直到拥有 1,000,000 个小专家，模型质量可能会无限提高。
百万专家混合论文提出了一种优化方法。假设我们有许多小专家𝑒ᵢ，每个专家都有一个固定的键𝑘ᵢ（只是一个常数向量）。让𝐾成为我们想要为每个标记使用的专家数量。
这篇论文中的 MoE 层的工作方式与 Mixtral 中的不同：
- 计算查询向量 𝑞(𝑥)，
- 计算标量积 𝑞(𝑥)ᵀ 𝑘ᵢ，
- 找到 𝐾 最大 𝑞(𝑥)ᵀ 𝑘ᵢ，
- 仅针对这些专家，计算路由器分数：𝑔ᵢ(𝑥) = 𝑠 (𝑞(𝑥)ᵀ 𝑘ᵢ)，
- 最后，输出为：
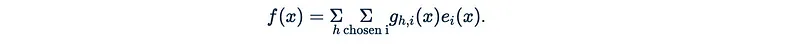
实际路由与向量数据库中的最近邻搜索非常相似。为此，我们有有效的算法，但由于我们需要对每个标记执行此操作，因此进一步优化它会更好。
作者建议使用乘积键，即取 𝑘ᵢ = (𝑐ᵢ, 𝑐’ᵢ)，即两个维度为 𝑘ᵢ 一半的键的串联。对于一百万专家来说，只有一千个不同的 𝑐ᵢ 就足够了。因此，我们不需要在一个 1,000,000 大小的数据库中进行最近邻搜索，而只需对两个 1,000 大小的数据库执行两次，这样效率要高得多。
作者甚至建议将专家 𝑒ᵢ 设置为一维（具有标量输出）。为了使 MoE 更具表现力，他们将其设置为多头：𝑞ₕ(𝑥)，
- 计算 𝐻 个独立查询向量 𝑞ₕ(𝑥)，
- 计算标量积 𝑞ₕ(𝑥)ᵀ𝑘ᵢ，
- 对于每个 ℎ，找到其自己的 𝐾 最大 𝑞ᵢ(𝑥)ᵀ 𝑘ᵢ 集，
- 仅针对这些专家，计算路由器分数：𝑔ₕ,ᵢ(𝑥) = 𝑠(𝑞ₕ(𝑥)ᵀ 𝑘ᵢ)，
- 最后，输出为：
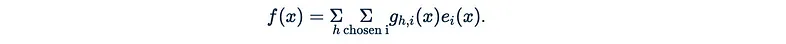
评估结果可以总结在以下图中：
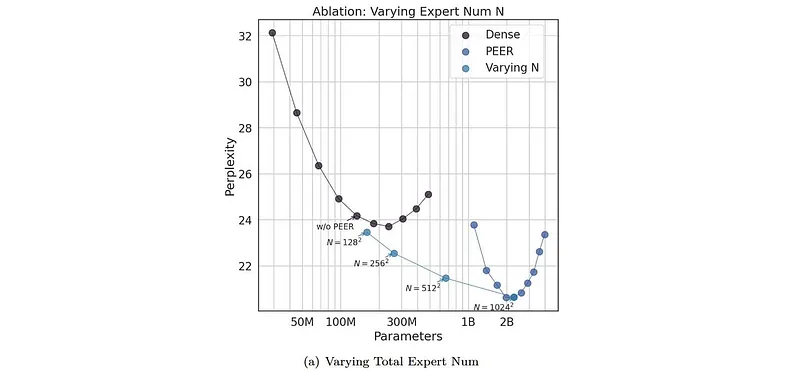
作者使用他们的方法，称为 PEER随着 N（微型专家的总数）增加到 102⁴²，能够实现困惑度的稳定改善。
要点：通过优化路由，MoE 可以稳步提高质量。
4、当许多专家都可以发挥作用时：终身学习案例
如果你有能力训练 LLM，可能希望每年左右创建一个新的 LLM，并具有新的架构优势等。 但是，在从头开始训练的阶段之间，你可能希望使用一些新数据更新现有的 LLM — 以使其适应新的数据分布。 简单地继续之前的训练过程有时可能会导致灾难性的遗忘。 LoRA 不太擅长掌握新知识。 那么你应该怎么做？
论文 使用分布专业专家进行终身语言预训练建议冻结 LLM 的现有部分，并用新专家和门控对其进行扩充：
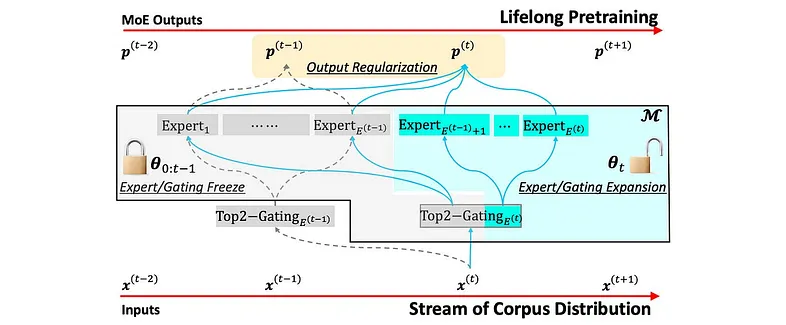
结果有些复杂，但总的来说，这个想法很有趣。
原文链接：Mixtures of Experts and scaling laws
汇智网翻译整理，转载请标明出处
