LLM推理的真相
当今人工智能领域最大的谎言是“自我修正”证明了大型语言模型(LLM)能够推理。但事实并非如此。
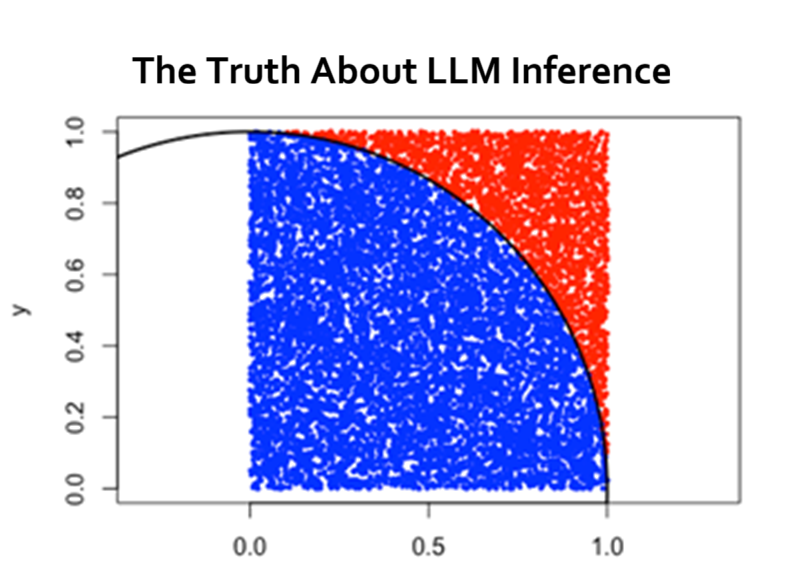
当今人工智能领域最大的谎言是“自我修正”证明了大型语言模型(LLM)能够推理。但事实并非如此:它只是在取平均值。
你问ChatGPT:“47 × 83是多少?”
它回答:“3901”
你说:“你确定吗?一步一步想想。”
现在它回应道:
Let me recalculate:
47 × 83
= 47 × (80 + 3)
= 47 × 80 + 47 × 3
= 3,760 + 141
= 3,901
Yes, I'm confident: 3,901大家都在庆祝:“看!AI 自我修正了!它在推理!”
我看着同样的互动,却看到了完全不同的东西:“AI 只是进行了蒙特卡洛估计,并将误差降低了 1/√N。它只是在做统计,而不是推理。”
让我从第一原理开始解释一下原因。
1、现实生活中的例子:醉酒的飞镖投掷者
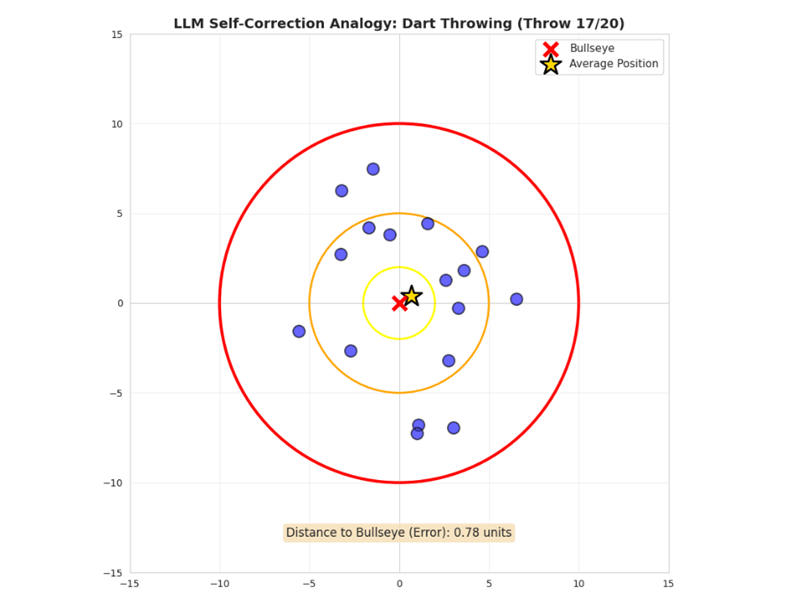
想象一下,你在一家酒吧。墙上挂着一个飞镖靶,靶心值 50 分。
你的朋友汤姆刚好喝了三杯啤酒。他酒量不大,也不太清醒。他拿起一支飞镖投了出去。
第一次投掷:飞镖落在距靶心6英寸的地方。他得了15分。
你问:“汤姆,你能射中靶心吗?”
他说:“看这个。”他又投了一次。
第二次投掷:飞镖落在距靶心8英寸的地方。他得了10分。
第三次投掷:距离靶心4英寸。得了25分。
第四次投掷:距离靶心5英寸。得了20分。
他每次投掷都没能射中靶心。但有一点很有意思:
如果计算四支飞镖的平均位置,平均距离靶心只有2.3英寸。
汤姆每次投掷都没能射中靶心,但通过平均四次投掷,他离目标更近了。
这就是 ChatGPT “自我修正”的本质。
让我来给你展示一下其中的数学原理。
2、设置:当你问一个问题时会发生什么
当你向 ChatGPT 提问时,底层会发生一些特定的事情。
该模型会计算所有可能答案的概率分布:
P(A|Q)
其中:
- Q 是你的问题
- A 是答案
- P(A|Q) 是给定问题 Q 得出答案 A 的概率
对于我们的乘法示例:“47 × 83 是多少?”,模型可能会计算:
P(3,901 | Q) = 0.42
P(3,891 | Q) = 0.18
P(3,911 | Q) = 0.15
P(4,001 | Q) = 0.09
P(3,801 | Q) = 0.08
... (infinite other possibilities)然后,模型会从该分布中抽样。它会根据这些概率选择一个答案。
想象一下汤姆投掷一支飞镖。飞镖落在某个地方,但这对他试图投掷的位置是一个噪声估计。
让我们用数学形式化地表达这一点。
3、数学框架:将答案建模为随机变量
将问题 Q 的真实答案定义为:
A = 真实答案*
例如:A* = 3,901
当 LLM 生成答案时,它会产生:
 ~ P(A|Q)
其中 Â是从概率分布中采样的随机变量。
该随机变量有两个关键属性:
- 期望值(均值):
E[Â] = Σ(a · P(a|Q))
如果模型训练良好,并且问题在其知识范围内(参见我之前的文章),则:
E[Â] ≈ A*
平均答案接近真实答案,但任何单个样本都可能相差甚远。
- 方差:
Var(Â) = E[( Â — E[Â])²] = σ²
这衡量了答案的分散程度。高方差意味着模型不确定——它的猜测到处都是。
让我们用数字来具体说明这一点。
4、具体示例:计算方差
假设 ChatGPT 对“47 × 83”的内部分布如下:
| 答案 | 概率 |
|---|---|
| 3,901(正确) | 0.42 |
| 3,891 | 0.18 |
| 3,911 | 0.15 |
| 4,001 | 0.09 |
| 3,801 | 0.08 |
| 3,951 | 0.05 |
| 3,851 | 0.03 |
首先,计算期望值:
E[Â] = Σ(Aᵢ · P(Aᵢ))
= 3,901 × 0.42 + 3,891 × 0.18 + 3,911 × 0.15 + 4,001 × 0.09 + 3,801 × 0.08 + 3,951 × 0.05 + 3,851 × 0.03
= 1,638.42 + 700.38 + 586.65 + 360.09 + 304.08 + 197.55 + 115.53
= 3,902.7期望值为 3,902.7——非常接近真实答案 3,901。
但问题在于:你只有一个样本。
ChatGPT 生成答案时,它不会给出 E[Â]。它会根据这个分布给你一个样本——可能是 3,891,可能是 4,001,也可能是 3,901。
方差告诉你这个样本的风险有多大。
计算方差:
Var(Â) = E[( Â — E[Â])²]
= (3,901–3,902.7)2 × 0.42 + (3,891–3,902.7)2 × 0.18 + (3,911–3,902.7)2 × 0.15 + (4,001–3,902.7)2 × 0.09 + (3,801–3,902.7)2 × 0.08 + (3,951–3,902.7)² × 0.05 + (3,851–3,902.7)² × 0.03
= (-1.7)² × 0.42 + (-11.7)² × 0.18 + (8.3)² × 0.15 + (98.3)² × 0.09+(-101.7)²×0.08+(48.3)²×0.05+(-51.7)²×0.03
= 2.89 × 0.42 + 136.89 × 0.18 + 68.89 × 0.15 + 9,662.89 × 0.09 + 10,342.89 × 0.08 + 2,332.89 × 0.05 + 2,672.89 × 0.03
= 1.21 + 24.64 + 10.33 + 869.66 + 827.43 + 116.64 + 80.19
= 1,930.1所以: σ² = 1,930.1
标准差: σ = √1,930.1 ≈ 43.9
这意味着当 ChatGPT 回答一次后,其答案通常在正确答案的 ±44 分范围内。
对于 47 × 83 = 3,901,一个答案可能会给出 3,857 到 3,945 之间的任意分数。
这是一个很大的误差范围。
现在,事情变得有趣了。
5、解决方案:多次采样(自我修正的错觉)
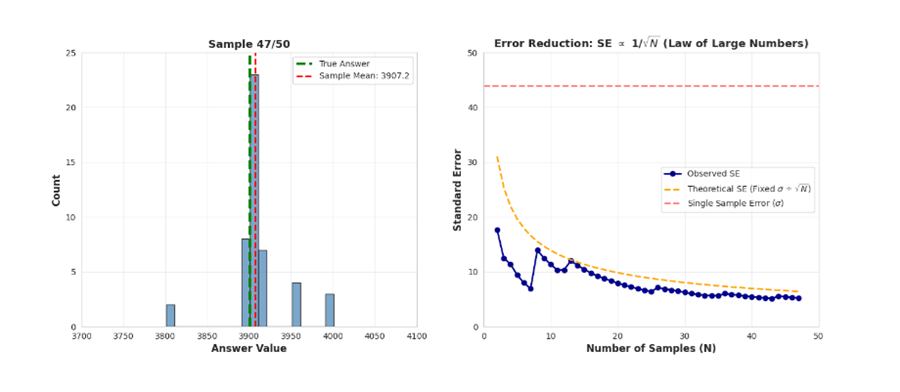
如果你不是问一次,而是让 ChatGPT 回答 N 次呢?
你可能会说:
- “47 × 83 是多少?” → 回答 1
- “你确定吗?重新计算。” → 回答 2
- “一步一步思考。” → 回答 3
- “验证你的计算。” → 答案 4
每个问题都会生成一个新的样本:₁、₂、₃、₄
现在取平均值:
Ā = (₁ + ₂ + ₃ + ₄) / 4
这个平均值是一个新的随机变量。关键在于:
平均值的方差远小于单个样本的方差。
让我从数学上解释一下原因。
6、大数定律(18 世纪的魔法)
假设你有 N 个来自同一分布的独立样本:
Â₁, Â₂, …, Âₙ
每个样本的分布如下:
- 期望值:E[Âᵢ] = μ
- 方差:Var(Âᵢ) = σ²
定义样本均值:
Ā = (Â₁ + Â₂ + … + Âₙ) / N
样本均值的期望值为:
E[Ā] = E[(Â₁ + Â₂ + … + Âₙ) / N]
= (E[Â₁] + E[Â₂] + … + E[Âₙ]) / N
= (μ + μ + … + μ) / N
= Nμ / N
E[Ā] = μ
平均值是无偏的——它仍然指向真实答案。
但魔法就在这里。计算样本均值的方差:
Var(Ā) = Var[(₁ + ₁ + … + ₙ) / N]
= (1/N²) × Var(₁ + ₁ + … + ₙ)
如果样本独立:
= (1/N²) × [Var(₁) + Var(₁) + … + Var(ₙ)]
= (1/N²) × [σ² + σ² + … + σ²]
= (1/N²) × Nσ²
Var(Ā) = σ² / N
方差随 N 的增加而线性下降!
标准差(标准误差)变为:
SE(Ā) = σ / √N
这就是著名的大数定律。
随着 N 的增加,样本均值收敛于真实均值,不确定性缩小 1/√N。
让我来演示一下这对我们的例子意味着什么。
7、具体计算:通过自我修正减少误差
记住:对于单个答案,σ = 43.9。
N = 1 个样本(一个答案):
SE = 43.9 / √1 = 43.9
预期误差:±43.9 分
N = 4 个样本(四次尝试):
SE = 43.9 / √4 = 43.9 / 2 = 21.95
预期误差:±22 分
误差下降了 50%!
N = 9 个样本:
SE = 43.9 / √9 = 43.9 / 3 = 14.63
预期误差:±15 分
误差下降了 67%!
N = 16 个样本:
SE = 43.9 / √16 = 43.9 / 4 = 10.98
预期误差:±11 分
误差下降了 75%!
这就是“自我修正”有效的原因。并非因为 AI 会推理,而是因为你生成了多个噪声样本并取平均值,这在数学上将误差降低了 1/√N。
这和汤姆的平均飞镖位置比任何一次投掷都更接近靶心的原因是一样的。
但是等等——这里有个陷阱。
8、隐藏的问题:样本并非独立(相关陷阱)
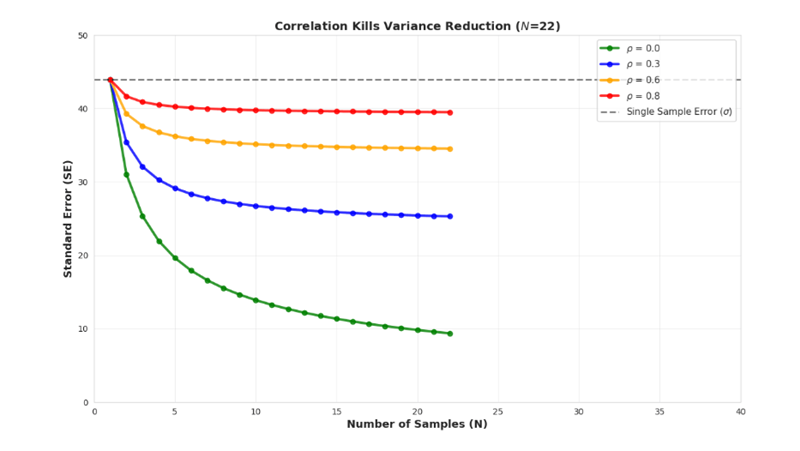
我刚才展示的所有内容都假设样本是独立的——₁、₂、₃、₄ 就像四次独立的抛硬币。
但事实并非如此。
当你问 ChatGPT 四次:
- “47 × 83 是多少?”
- “你确定吗?重新计算。”
- “一步一步思考。”
- “验证你的工作。”
这四个答案都来自同一个模型,具有相同的权重、相同的偏差和相同的训练数据。
它们不是从 P(A|Q) 中独立抽取的。它们是相关的抽取。
从数学上讲,如果样本与相关系数 ρ 相关,方差公式就会发生变化:
Var(Ā) = σ²/N + (σ²/N) × ρ × (N-1)
简化:
Var(Ā) = (σ²/N) × [1 + ρ(N-1)]
如果 ρ = 0(独立样本):Var(Ā) = σ²/N(我们之前计算的结果)
如果 ρ = 1(完全相关):Var(Ā) = σ²(没有任何改进!)
真正的 LLM 样本的 ρ 值在 0 < ρ < 1 之间。它们是部分相关的。
假设 ρ = 0.6(对于“思路链”样本来说,这是一个合理的估计值)。
当 N = 4 且 ρ = 0.6 时:
Var(Ā) = (σ²/4) × [1 + 0.6 × 3]
= (σ²/4) × [1 + 1.8]
= (σ²/4) × 2.8
= 0.7σ²
标准误差:SE = √(0.7σ²) = 0.837σ
与独立样本的 SE = σ/2 = 0.5σ 不同,我们得到的 SE = 0.837σ。
改进率仅为 16%,而不是 50%!
这就是为什么自校正在 2-3 次迭代后收益递减的原因。
有效样本量为:
Nₑff = N / [1 + ρ(N-1)]
当 ρ = 0.6 且 N = 4 时:
Nₑff = 4 / [1 + 0.6 × 3] = 4 / 2.8 = 1.43
你得到的只是相当于 1.43 个独立样本的信息量,而不是 4 个。
这就是为什么 o1 在经过几个思考步骤后就停止改进的原因。它达到了相关性极限。
9、思维链的联系(为什么思维链是蒙特卡洛抽样)
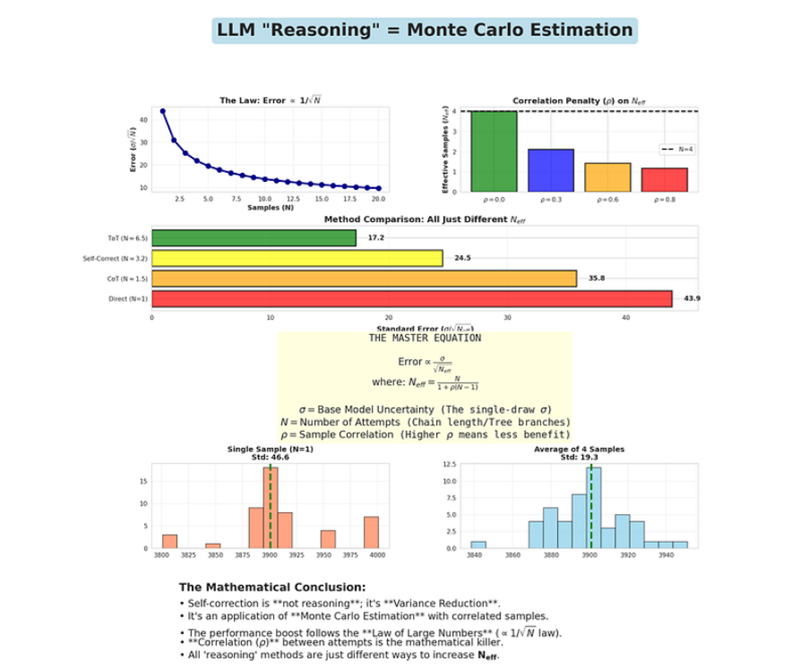
现在让我们将其与思维链 (CoT) 提示联系起来。
当你说“一步一步思考”时,你并不是在要求模型进行推理。你是在要求它生成一个扩展的样本轨迹。
没有思维链:
Q:“47 × 83 是多少?” A:一次采样一个 token → “3,901”
这是穿过模型概率空间的一条样本路径。
使用 CoT:
Q:“47 × 83 是多少?一步一步思考。” A:采样扩展轨迹:
"Let me calculate:
47 × 80 = 3,760
47 × 3 = 141
3,760 + 141 = 3,901"这仍然是一条样本路径,但它是一条更长、更受约束的路径。
通过强制使用模型生成中间步骤,您将:
- 降低每一步的方差(标记越小,不确定性越小)
- 创建隐式检查点,引导样本趋向于误差较小的区域
- 在一个响应中生成多个子样本
从数学上讲,CoT 等价于:
- 无 CoT:一步采样,方差为 σ²
- 有 CoT:分 k 步采样 ₁、₁₂、…、ₖ,然后计算 Â = f(Â₁, …, Âₖ)
如果每个子步骤的方差为 σ²/k,则最终方差约为:
Var(Â_CoT) ≈ σ²/k
对于 k = 10 个中间推理步骤:
SE_CoT = σ / √10 ≈ 0.316σ
与直接回答相比,CoT 将误差降低了 68%!
但这不是推理。它通过蒙特卡洛抽样来减少方差。
10、思维树:显式蒙特卡洛抽样
思维树 (ToT) 使这一点更加明确。
ToT 生成多条推理路径:
Path 1: 47×80=3,760, 47×3=141, total=3,901
Path 2: 50×83=4,150, subtract 3×83=249, total=3,901
Path 3: 40×83=3,320, add 7×83=581, total=3,901然后它会选择最常见的答案(或得分最高的路径)。
这实际上是蒙特卡洛估计:
- 生成 N 个样本(推理路径)
- 评估每个样本(对每条路径进行评分)
- 汇总结果(选择最佳或平均)
误差减少遵循相同的 1/√N 定律——直到相关性开始显现。
11、中心极限定理(最终结论)
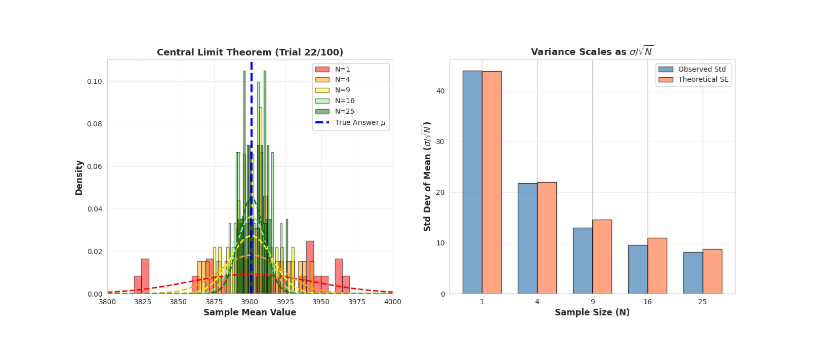
统计学中还有一个更精彩的结果可以解释其工作原理。
中心极限定理指出:
如果从均值为 μ、方差为 σ² 的任意分布中抽取 N 个独立样本,则样本均值 Ā 服从正态分布: Ā ~ N(μ, σ²/N)
当 N → ∞ 时,Ā 的分布变为:Ā → N(μ, 0)
样本均值收敛于 μ 处的一点,方差为零。
原因如下:
- 1 个样本:噪声非常大
- 4 个样本:噪声中等
- 16 个样本:相当准确
- 100 个样本:非常准确
分布形状缩小了 1/√N。
以 σ = 43.9 为例:
- N = 1:Ā ~ N(3,901, 43.⁹²) → 95% 置信区间:[3,815, 3,987]
- N = 4:Ā ~ N(3,901, 2²²) → 95% 置信区间:[3,858, 3,944]
- N = 16:Ā ~ N(3,901, 1¹²) → 95% 置信区间:[3,880, 3,922]
经过 16 个自校正步骤,95% 的准确率下,您的准确率与真实答案的误差在 ±21 分以内。
这是“推理”背后的数学保证。
12、为什么这能解释LLM的一切
现在我们可以解释所有“推理”现象了:
为什么“一步一步思考”有效?
它通过多个隐式检查点生成更长的样本轨迹,将方差从 σ² 降低到大约 σ²/k。
为什么自我修正提示能提高准确率?
它们生成额外的相关样本,将标准误差从 σ 降低到 σ/√Nₑff。
为什么 OpenAI o1 的“思考”时间更长?
它生成了更多样本(在思考阶段使用更多 token),从而提高 N 以减少误差。
为什么 o1 的收益递减?
样本相关性 ρ 限制了有效样本量:Nₑff = N/[1 + ρ(N-1)]
为什么集成方法(N 中取最优)有效?
纯蒙特卡洛方法:生成 N 个样本,挑选最佳样本。对于独立样本,误差降低恰好为 1/√N。
为什么温度会影响质量?
温度控制 σ²(分布的方差)。温度降低 → σ 降低 → 每个样本的误差降低。但这不会改变 N 的缩放比例。
13、统领一切的公式
以下是 LLM 准确度的主公式:
误差 = σ / √Nₑff
其中:
- σ = 基础模型不确定性(取决于:模型大小、训练数据、温度、提示质量)
- Nₑff = 有效样本数 = N / [1 + ρ(N-1)]
- N = 尝试次数(直接答案、CoT 步骤、自我修正、ToT 路径)
- ρ = 样本间相关性(对于典型的 CoT/自我修正,相关性约为 0.5-0.8)
想要更准确的答案?你有三个杠杆:
- 降低 σ:更好的训练、更好的提示、更低的温度、RAG
- 增加 N:更多自我修正、更长的 CoT、思维树
- 降低 ρ:使样本更独立(更难——需要架构更改)
就是这样。这就是整个游戏。
14、这对你意味着什么
下次有人告诉你“大模型可以推理”时,想想汤姆投掷飞镖的情景。
汤姆并不是通过更努力地思考来提高他的瞄准能力。他通过投掷更多飞镖来提高他的平均准确率。
飞镖是相关的(同一个投掷者、相同的醉酒程度、相同的技巧),所以这种改进不如独立投掷那么好。但取平均值仍然有帮助。
LLM也一样。它们在自我修正时不会“推理”。它们在概率空间中采样多个相关的轨迹,并取平均结果。
数学很优美。改进是真实的。但这不是推理。
这是大数定律——一个源自1713年(雅各布·伯努利)的成果,披着2025年的外衣。
它的架构是现代的。其底层力量是纯粹的基础统计学。
在我们构建出真正知道自己何时不知道的人工智能之前,每一个“推理突破”都只不过是另一种生成更多样本并进行平均的巧妙方法。
数学是无情的。昏暗的最终回报是不可避免的。相关性壁垒是真实存在的。
代码爱好者可以尝试以下 Playground:
AIMathematicallyexplained/LLM_Reasoning_Statistics_Playground.ipynb at main · MLDreamer/AIMathematicallyexplained · GitHub
原文链接:LLM Self-Correction is a Myth: Your AI isn't Reasoning, It's Just Averaging
汇智网翻译整理,转载请标明出处
